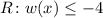To make things easier, convert the form of the function, from algebraic to root
![\begin{gathered} w(x)=-(3x)^{(1)/(2)}-4 \\ w(x)=-\sqrt[]{3x}-4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5mxkmnozhyufvkitl4zbhg9ddcnmrlhuix.png)
For this function, the domain can't include negative values due to the square root. It means
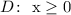
To define the range, evaluate the function in the lower value of the domain (which is 0)
![\begin{gathered} w(0)=-\sqrt[]{3\cdot0}-4 \\ w(0)=-4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9cegylbi7ccc1v2t2q78msspf45pot0i3h.png)
The range include all values that are less than or equal to -4