Solution
Step 1
Choose a method to solve the quadratic equation and state it
For this problem, we will differentiate the given equation to find the maximum value

Step 2
find the value of x, knowing that at the maximum point of the profit the equation we got after differentiation = 0
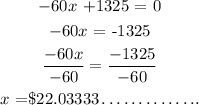
To the nearest cent, the price of one widget for maximum profit is $22.03