Question

Can Someone help me with number 4 i dont understand

Answer 1

Two lines are parallel if their slopes are equal.

In this case we have the lines:

`\begin{gathered} y-7x=6 \\ y+7x=8 \end{gathered}`

If we rearrange them in slope-intercept form, we get:

`\begin{gathered} a)y-7x=6\longrightarrow y=7x+6 \\ b)y+7x=8\longrightarrow y=-7x+8 \end{gathered}`

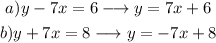
As line a has a slope m=7 and line has a slope m=-7, the lines have different slopes so they are not parallel.

`\begin{gathered} m_a=7 \\ m_b=-7 \\ 7\\eq-7\longrightarrow\text{not parallel} \end{gathered}`

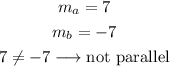
Answer: The lines are not parallel