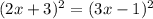
start by expanding both sides of the equation
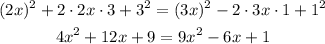
bring all to the left side of the equation

switch the signs of the equations
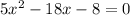
write -18x as a difference
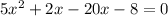
factor x and factor -4
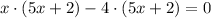
factor '5x+2' of the expression
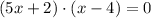
when a product of two factors is equal to 0, at least one of the factors is 0, then equal each to 0 and solve for x
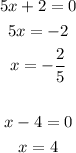
the solutions to the equation are 4 and -2/5.