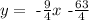Question

• Write the equation of the line that passes through the points (-7,0) and(-3,-9). Put your answer in fully reduced point-slope form.

Answer 1

We want to calculate the line that passes through the points (-7,0) and (-3,-9). Recall that the equation of a line is

`y=mx+b`

where m is the slope and b is the y intercept. We can calculate first the slope and then find the value of b. To do so, recall that given points (a,b) and (c,d) the slope of the line that passes through them is given by the formula

`m=\frac{(d\text{ -b)}}{(c\text{ -a)}}=\frac{b\text{ -d}}{a\text{ -c}}`

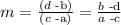
so by taking a=-7, b=0, c=-3 and d=-9 we get

`m=\frac{0\text{ - (-9)}}{\text{ -7 -( -3)}}=\frac{9}{\text{ -4}}=\text{ -}(9)/(4)`

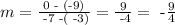
so our equation becomes

`y=\text{ -}(9)/(4)x+b`

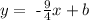
so know we want this line to pass through the point (-7,0), so whenever x= -7 then y=0 so we have the equation

`0=\text{ -}(9)/(4)(\text{ -7)+b}`

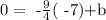
or equivalently

`0=(63)/(4)+b`

so if we subtract 63/4 on both sides, we get

`b=\text{ -}(63)/(4)`

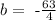
so our equation would be

`y=\text{ -}(9)/(4)x\text{ -}(63)/(4)`