Question

The US Department requires that pasteurized milk contain no more than 20,000 bacteria per milliliter. It has been established that the number of bacteria in milk stored at 4.5 ° C can double in 39 hours. If after pasteurization, a sample of milk contains 20,000 bacteria per milliliter, what will be the number of bacteria per milliliter after 10 days?

Answer 1

Step 1 - Find a formula to solve the problem

Since we know the number of bacteria per milliliter doubles each 39 hours, we expect it to be a exponential growth, with 2 being the exponent (because it always doubles at a definite time interval). Such a problem can be solved by an equation like this one:

`N_t=N_0*2^(t/T)`

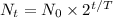
In the equation above, Nt represents the number of bacteria per milliliter at time t, whereas N0 is the initial amount of bacteria per milliliter. T represents the time it takes for the number of bacteria per milliliter to double.

Step 2 - Substitute the numerical values and work the math

According to the exercise, t = 240 h (10 days), T = 39 h, N0 = 20000 bacteria per milliliter. Substituting these values on the equation above:

`N_t=20000*2^(240/39)`

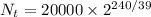
Working the numbers, we have:

`N_t=20000*2^(6.1)=20000*68.6=1.3*10^6\text{ bacteria per milliliter}`

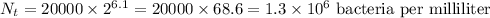
So, after 10 days, there will be aproximmately 1 billion bacterias per milliliter.