The sum of the digits
 ,
,
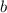 , and
, and
 is
is
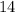 .
.
The image appears to show a column addition problem with missing digits represented by a, b, and c:
9 a 1
+ 7 2 b
------------
c 8 2
To solve this, we follow the standard procedure for addition, starting from the rightmost column:
1. In the rightmost column,
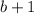 must equal 2, or result in 2 when 10 is subtracted (if there's a carry-over from the middle column). Since there's no carry-over mentioned, and b is a single digit,
must equal 2, or result in 2 when 10 is subtracted (if there's a carry-over from the middle column). Since there's no carry-over mentioned, and b is a single digit,
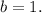
2. In the middle column,
 must give us the units digit of 8. Since
must give us the units digit of 8. Since
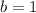 , and there's no carry-over from the rightmost column,
, and there's no carry-over from the rightmost column,
 must be 6 to make
must be 6 to make
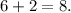
3. In the leftmost column, we add 9 and 7 to get 16. The digit 'c' in the sum must be 1 more than the 10's place of this sum due to the carry-over from the middle column (if any). Since 9 + 7 = 16, there is a carry-over, and so
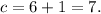
Now we can sum a, b, and c:
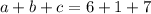
Calculating this, we get:
The sum of the digits
 ,
,
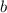 , and
, and
 is
is
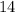 .
.