An exponential function is modeled using the equation:
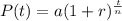
where P(t) is the population after t years, a is the initial population, r is the growth rate in decimals, t is the number of years, and n is the number of periods in one cycle.
From the given information, we have the following parameters:
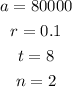
Therefore, the population after 8 years can be calculated by substituting into the formula and solving for P(t) as follows:
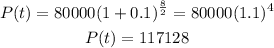
The population is 117,128.