1 Answer

Aprillion · Answer 1 · 2023-02-14T23:56:28+0000

Noah's score = 92

Noah's class mean = 81

Noah's class standard deviation = 5.1

Thus, his z-score his calculated as;

$\begin{gathered} z=(x-\mu)/(\sigma) \\ \text{Where }\mu=\operatorname{mean} \\ \sigma=\text{ standard deviation} \end{gathered}$

Thus, for Noahs', we have;

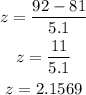
$\begin{gathered} z=(92-81)/(5.1) \\ z=(11)/(5.1) \\ z=2.1569 \end{gathered}$

Also, similarly for Amelia, we have;

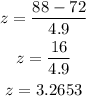
$\begin{gathered} z=(88-72)/(4.9) \\ z=(16)/(4.9) \\ z=3.2653 \end{gathered}$

From the results above, Amelia's z-score is higher than that of Noah. Thus, Amelia relatively has the higher score.

Please log in or register to add a comment.