Question

A bag contains 7 red balls and 3 white balls. Andrew,Betsy, Cam and Doug, in that order. are going to randomlypick a ball out of the bag and not replace it. The firstperson to draw a white ball wins SI60. What is theprobability that Doug will win the S160?

Answer 1

We have the following events:

`\begin{gathered} R_1=\text{Andrew picks a red ball} \\ R_2=\text{Betsy picks a red ball} \\ R_3=\text{Cam picks a red ball} \\ R_4=\text{Doug picks a white ball} \end{gathered}`

since the game is without replacement, then the probabilites are:

`\begin{gathered} P(R_1)=(7)/(10) \\ P(R_2)=(6)/(9) \\ P(R_3)=(5)/(8) \\ P(R_4)=(3)/(7) \end{gathered}`

therefore, if we calculate the probability of the intersection of these events (since we want them to happen at the same time) we get:

`P(R_1\cap R_2\cap R_3\cap R_4)=(7)/(10)\cdot(6)/(9)\cdot(5)/(8)\cdot(3)/(7)=(630)/(5040)=(1)/(8)_{}`

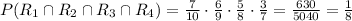
Therefore, the probability that Doug win the $160 is 1/8