Question

Find the angle 6,700ft to 3250 ft between two lines of the sight of a peak

Answer 1

Part A:

In a semicircle, you have an angle of pi radians, then, the total angle given by the sum of 1.10 radians, the angle between the sight of the peaks and 0.84 radians should be equal to pi.

`1.10+0.84+x=\pi`

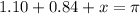
Solving for x:

`x=\pi-1.94\approx1.20`

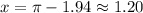
Then, the angle between those peaks is 1.20 radians

Part B:

The vertical projection of each diagonal(as you can see on the image below) is given by the sine function. If we calculate the sine function for the angles times the diagonal we're going to find the height.

Then, to the smaller peak, we have the following formula

`h_1=3250*\sin (0.84)\approx2420.09`

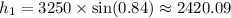
To the bigger peak

`h_2=6700*\sin (1.10)\approx5971.09`

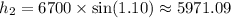
With this, we have the height for both summits.

Summit of the smaller peak = 2420.09 ft

Summit of the bigger peak = 5971.09 ft

Part C:

The vertical projection of each diagonal is given by the sine function, as we used in the previous question, and the horizontal projection is given by the cosine function(also noted in the previous image).

If we have the horizontal projection of both diagonals and sum them, we're going to have the distance between the summits of each peaks.

`\begin{gathered} d_1=3250*\cos (0.84)\approx2169.25 \\ d_2=6700*\cos (1.10)\approx3039.09 \\ d_1+d_2=5208.34 \end{gathered}`

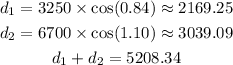
With this, we have our distance. The distance between the summits of each peak is 5208.34 ft.