SOLUTION
We will consider all the sets of probabilities, the one with the highest probability is the right answer.
a) You roll an odd number and roll a 5: the probability is calculated thus:
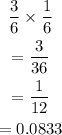
b) You land on an odd number or you roll a 6: the probability is calculated thus:
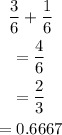
c) You roll a six and roll a 4: the probability is calculated thus:
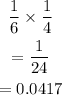
d) You roll a 3 and roll an old number: the probability is calculated thus:

Now, comparing all the probabilities, the set of independent events with the highest probability is the event of You land on an odd number or you roll a 6.
Therefore the correct answer is B.