We can express this as a system of equations.
Let x be the liters of the 50%-acid solution and y the liters of the 75%-acid solution.
We then need 2 equations to solve this.
One equation is the total amount of liters (70 liters) that is equal to the sum of the amount of each solution:

The second equation is the final concentration, that is a weighted average of the concentration of each solution:
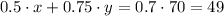
Then, we can solve this by substitution:

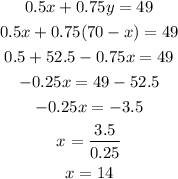
Then, we can calculate y as:
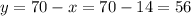
Answer: we need 14 liters of the 50% acid solution and 56 liters of the 75% acid solution.