Question

Personal finance Funding a retirement goal. Austin Miller wishes to have $800,000 in a retirement fund 20 years from now. He can create the retirement fund by making a single lump-sum deposit today.   If upon retirement in 20 years, Austin plans to invest $800,000 in a fund that earns 4 percent, what is the maximum annual withdrawal he can make over the following 15 years?

Answer 1

Answer: $71942.45

We can solve this problem by using the following formula:

`\text{PMT}=\frac{PV}{PVA\text{ factor}}`

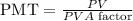
To solve for the PVA factor, we will use the formula,

`\text{PVA factor =}(1-(1+r)^(-n))/(r)`

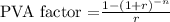
From the given problem, we know that:

r = 4% = 0.04

n = 15

Substituting this to our equation,

`=(1-(1+r)^(-n))/(r)=(1-(1+0.04)^(-15))/(0.04)=11.12`

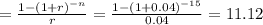
Now that we have our PVA factor, we can now solve for the PMT.

We now know that:

PV = $800000

PVA factor = 11.12

Substituting these to the equation:

`\text{PMT}=\frac{PV}{PVA\text{ factor}}`
`\text{PMT}=(800000)/(11.12)=71942.45`

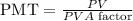
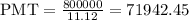
Hence, the maximum annual withdrawal he can make over the following 15 years is $71942.45