ANSWER and EXPLANATION
The polynomial has a degree of 3. This means that it has 3 roots.
Let the roots of the polynomial be a, b, and c such that:
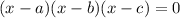
We are given two roots already (-1, 2). This implies that:
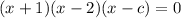
Expand the equation:
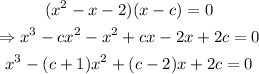
We are given the following conditions:
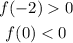
Applying the first condition:
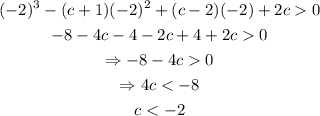
Applying the second condition:
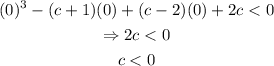
Therefore, we have that:
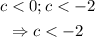
Therefore, the third root can take any values that are less than -2.