For the sequence 2, 4, 6, 8, 10......
You can observe that the common difference is 2
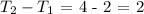
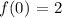
Since we already know that the common difference is 2, the recursive formula can be written generally as :
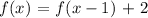
Where f(x) is the present term and f(x-1) is the preceding term
The equation written above is the linear equation in the recursive form.
For the explicit form of the linear equation
Since the common difference, d = 2. It is obvious that the equation is an AP
The general formula for an arithmetic progression is:
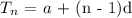
The first value, a = 2
The common diference, d = 2
The explicit form of the linear equation then becomes:
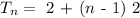
Where n is the number of terms in the sequence