Question

1. On the last 5 quizzes, Marco has earned a total of 21 out of 25 possible points. If he has a perfectscore on the next several quizzes, exactly how many points will he need to bring his average up to90%? (Note: you must use the techniques you learned in Unit 5 to earn credit on thisproblem.)(a) Write a rational equation to represent this situation. (2 points)

Answer 1

From the statement, we know that in the last 5 quizzes, Marco has earned 21 out of 25 possible points. If each quiz gives Marco the same possible points, each quiz can give Marco s = 5 possible points. We can write the following formula for the average:

`A=(S_1+S_2+\ldots+S_N)/(s\cdot N)\cdot100`

Where:

• S_1, S_2, ... are the scores that Marco obtains in each quiz,

,

• N is the total number of quizzes played by Marco,

,

• s = 5 is the max possible points that Marco can win in each quiz,

,

• the 100 is a factor to convert the average to %.

Now, we know that Marco obtained:

`S_1+S_2+S_3+S_4+S_5=21`

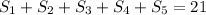
points in the 5 first quizzes.

If Marco has a perfect score on the next several quizzes, he will get:

`S_i=5,i\ge6.`

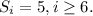
We must find how many points he will need to get an average A = 90.

We replace the data that we know in the formula above:

`\begin{gathered} \frac{(S_1+S_2+S_3+S_4+S_5)+(S_6+\cdots_{}+S_N)}{s\cdot N}\cdot100=90, \\ (21+5\cdot(N-5))/(5\cdot N)\cdot100=90. \end{gathered}`

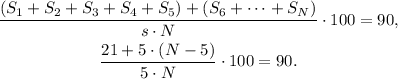
We solve the last equation for N:

`\begin{gathered} (21+5N-25)/(5N)\cdot100=90, \\ (5N-4)/(5N)=0.9, \\ 5N-4=0.9\cdot5N, \\ 5N-4=4.5N, \\ 0.5N=4, \\ N=(4)/(0.5)=8. \end{gathered}`

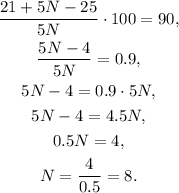
So Marco needs to play 48 games. The total points that he needs to play are:

`P=21+5(N-5)=21+5(8-5)=21+5\cdot3=36`

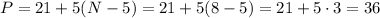
Answer: Marco will need to have 36 points in total in 8 quizzes to reach an average of 90%. He has played 5 quizzes and obtained 21 out of 25 possible points. So he will need to play 3 additional games with a perfect score of 5, getting 15 points to reach the average of 90%.