Question

For the exponential function f, find f^-1 analytically and graph both f and f^-1.f(x)=6^x-8

Answer 1

First, replace f(x) by y. This is done to make the rest of the process easier.

`y=6^x-8`

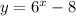
Now, replace every x with y and a every y with an x:

`x=6^y-8`

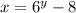
Now, solve this equation for y. Then, we must move -8 to the left hand side as +8. It yields

`x+8=6^y`

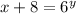
Now, we can apply logarithms in both sides:

`\log (x+8)=\log 6^y`

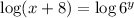
For the properties of logarithms, we have

`\log 6^y=y\log 6`

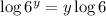
then, we have

`\log (x+8)=y\log 6`

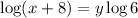
and we obtain

`y=(\log(x+8))/(\log6)`

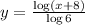
Finally, replace y with f^1. Then, the inverse funcion is

`f^(-1)(x)=(\log(x+8))/(\log6)`

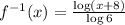
The graphs of the function and its inverse are: