Question

Two ships are sailing parallel to each other. The path of one ship is represented on a coordinate plane as the line y = –1/3x + 4. The second ship’s path passes through the point (3, 5). Select another point that the path of the second ship passes through.A.(0, 7)B.(6, 6)C.(–3, 7)D.(–4, 6)

Answer 1

Solve for the equation of the second line.

Since they are sailing parallel to each other, we can say that they have the same slope.

The slope of the first ship is

`\begin{gathered} y=mx+b \\ m\text{ is the slope} \\ b\text{ is the y-intercept} \\ \\ y=-(1)/(3)x+4 \\ m=-(1)/(3) \\ \\ \text{the slope is }-(1)/(3) \end{gathered}`

Use the coordinate (3,5) to solve for the equation of the second ship

`\begin{gathered} (x,y)=(3,5) \\ x=3,y=5 \\ m=-(1)/(3)(\text{same as the other ship}) \\ \\ y=mx+b \\ 5=(-(1)/(3))(3)+b \\ 5=-1+b \\ 5+1=b \\ b=6 \\ \\ \text{Therefore, the equation of the other line is } \\ y=-(1)/(3)x+6 \end{gathered}`

Test each point for which the second equation will satisfy

`\begin{gathered} \text{Test for (0,7)} \\ 7=-(1)/(3)(0)+6 \\ 7\\eq6 \\ \\ \text{Test for (6,6)} \\ 6=-(1)/(3)(6)+6 \\ 7=-2+6 \\ 7\\eq4 \\ \\ \text{Test for (-3,7)} \\ 7=-(1)/(3)(-3)+6 \\ 7=1+6 \\ 7=7 \\ \\ \text{Test for (-4,6)} \\ 6=-(1)/(3)(-4)+6 \\ 6=-(4)/(3)+6 \\ 6\\eq(14)/(3) \end{gathered}`

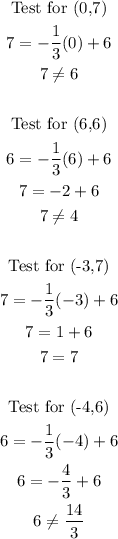
Therefore, the other point that the second ship will pass is (-3,7).