First we have to derivate the function
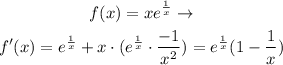
We have to find when the derivate is 0
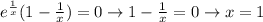
we have to consider x=0, because we can not divide by 0
so for a number lower than 0 we get that

so it is increasing
for a number between 0 and 1 we get
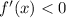
so it is decreasing
for a number greater than 1 we get

it is increasing