Question

Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem.f(x) = x^2 + x + 1, [0, 6], f(c) = 13c =

Answer 1

The given function is:

`\begin{gathered} f(x)=x^2+x+1 \\ \text{Interval } \\ \lbrack0,6\rbrack \end{gathered}`

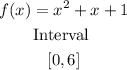
Start by evaluating the function in the extreme values of the interval:

`\begin{gathered} f(0)=0^2+0+1 \\ f(0)=1 \\ \text{And} \\ f(6)=6^2+6+1 \\ f(6)=36+6+1=43 \end{gathered}`

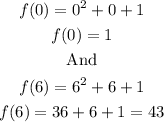
The intermediate value theorem states: if a function f is continuous in an interval [a,b], and k is any number between f(a) and f(b), then there exists a number c between a and b such that f(c)=k.

As k=13 and it is between 1 and 43, then there is a number c such that f(c)=13.

Now, replace f(c) by 13 and solve for c:

`\begin{gathered} 13=c^2+c+1 \\ \text{Subtract 13 from both sides} \\ 13-13=c^2+c+1-13 \\ 0=c^2+c-12 \end{gathered}`

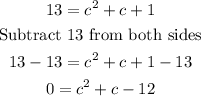
Let's find the factored form to find the c-values:

`\begin{gathered} c^2+c-12=(c+4)(c-3) \\ \text{Then equal both factors to zero and solve for c} \\ c+4=0 \\ c=-4 \\ \text{and} \\ c-3=0 \\ c=3 \end{gathered}`

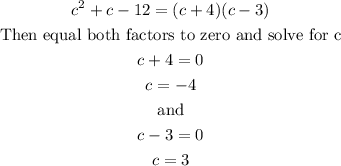
As -4 is not in the interval, thus the value of c guaranteed by the theorem is c=3.