Question

how fast is the angle of depression of the telescope changing when the boat is 190 meters from the shore

Answer 1

- 0.01943 rad/sec

Explanation:

The first thing is to make a drawing of what is mentioned in the statement, it would be the following:

Now, we have the following information:

`\begin{gathered} (dy)/(dt)=15\text{ m/s} \\ x=50\text{ m} \\ y=190\text{ m} \end{gathered}`

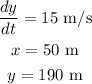
In this right angle triangle formed by telescope of the boat, e can apply the tangent trigonometric ratio, like this:

`\begin{gathered} \tan \theta=(x)/(y) \\ \text{ replacing} \\ \theta=\tan ^(-1)\mleft((x)/(y)\mright) \end{gathered}`

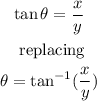
Now, we implicitly derive with respect to t:

`\begin{gathered} (d)/(dt)(\theta)=(d)/(dt)(\tan ^(-1)((x)/(y))) \\ (d)/(dt)(\theta)=(1)/(1+((x)/(y))^2)\cdot(d)/(dt)((x)/(y)) \\ (d)/(dt)(\theta)=(y^2)/(x^2+y^2)\cdot x\cdot(-(1)/(y^2)\cdot(dy)/(dt)) \\ (d)/(dt)(\theta)=(-x)/(x^2+y^2)((dy)/(dt)) \\ \text{ replacing} \\ (d)/(dt)(\theta)=(-50)/(50^2+190^2)\cdot(15) \\ (d)/(dt)(\theta)=-0.01943 \end{gathered}`

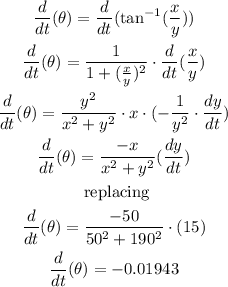
The angle of depression is changing at a rate of -0.01943 rad/sec when the boat is 190 m from the shore