Question

Hello! Would like help on parts b and c. Thank you!

Answer 1

The function given describes the difference in lenght after theta seconds:

`f(\theta)=2sin\theta+\sqrt[\placeholder{⬚}]{2}`

Part A:

When the pogo stick's spring is equal to its no compressed lenght is when the difference is equal to 0.

therefore, We have to do f(theta)=0.

`\begin{gathered} f(\theta)=0 \\ 2sin\theta+\sqrt[\placeholder{⬚}]{2}=0 \\ \end{gathered}`

Solving for theta:

`\begin{gathered} 2sin\theta=-\sqrt[\placeholder{⬚}]{2} \\ sin(\theta)=\frac{-\sqrt[\placeholder{⬚}]{2}}{2} \\ \theta=sin^(-1)(\frac{-\sqrt[\placeholder{⬚}]{2}}{2})=-(1)/(4)\pi \end{gathered}`

Part B:

If theta is equal to 2*theta in the interval [0,2pi)

`f(2\theta)=2sin2\theta+\sqrt[\placeholder{⬚}]{2}`

Evaluating in 0 and 2pi:

`\begin{gathered} f(0)=2s\imaginaryI n2*0+√(2)=2*0+\sqrt[\placeholder{⬚}]{2}=\sqrt[\placeholder{⬚}]{2} \\ f(2(2\pi))=2s\imaginaryI n2*2\pi+√(2)=2*sin4\pi+\sqrt[\placeholder{⬚}]{2}=2*0+\sqrt[\placeholder{⬚}]{2} \\ f(2*(\pi)/(2))=2s\imaginaryI n2*(\pi)/(2)+√(2)=2*sin\pi+\sqrt[\placeholder{⬚}]{2}=2*0+\sqrt[\placeholder{⬚}]{2} \end{gathered}`

Is the same than the original function because the sin of (2n*pi) is going to be always 0.

Part C:

Given the function for the another pogo:

`g(\theta)=1-cos^2\theta+\sqrt[\placeholder{⬚}]{2}`

As you can see, by trigonometric identity, we can rewrite the function g of the following way:

`\begin{gathered} sin^2\theta+cos^2\theta=1 \\ sin^2\theta=1-cos^2\theta \end{gathered}`

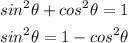
Substituing:

`g(x)=sin^2+\sqrt[\placeholder{⬚}]{2}`

Matching g and f:

`\begin{gathered} sin^2\theta+\sqrt[\placeholder{⬚}]{2}=2sin\theta+\sqrt[\placeholder{⬚}]{2} \\ sin^2\theta=2sin\theta \\ sin\theta=2 \end{gathered}`

Both length will be equal when the sin of theta is equal to 2.