Question

11. Find the length of the missing side. 16 25 19

Answer 1

x = 14.12

Step-by-step explanation:

To find the missing side, we will use the cosine law:

`c^2=a^2+b^2-2ab\cos (C)`

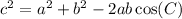
Where a, b, and c are the length of the sides of the triangle and C is the measure of the angle formed by the sides a and b.

So, we can use the equation to find the angle formed by the side of length 35 and the side of length 44 (25 + 19 = 44). So, replacing a by 35, b by 44, and c by 16, we get:

`16^2=35^2+44^2-2(35)(44)\cos (\theta)`

Then, solving for θ, we get:

`\begin{gathered} 256=1225+1936-3080\text{cos(}\theta) \\ 256=3161-3080\cos (\theta) \\ 256-3161=-3080\cos (\theta) \\ -2905=-3080\cos (\theta) \\ (-2905)/(-3080)=\cos (\theta) \\ 0.9432=\cos (\theta) \\ \cos ^(-1)(0.9432)=\theta \\ 19.41=\theta \end{gathered}`

Now, we can calculate the length of the missing side, using the angle θ = 19.41°, the side with length 35 and the side with length 25 as:

`x^2=35^2+25^2-2(35)(25)\cos (19.41)`

Therefore, the value of x is:

`\begin{gathered} x^2=1225+625-1650.56 \\ x^2=199.44 \\ x=\sqrt[]{199.44} \\ x=14.12 \end{gathered}`

So, the length of the missing side is 14.12