Given:
The coordinates of C, the midpoint of AB, (X, Y)=(1, 5).
The coordinates of A, (x1, y1)=(3, 2).
Let the coordinates of B be (x2, y2).
The midpoint formula is given by,

Hence,
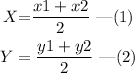
Substitute the known values in equation (1) and solve for x2.
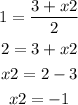
Hence, x2=-1.
Substitute the known values in equation (2) and solve for y2.
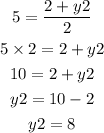
Therefore, the coordinates of point B is (x2,y2)=(-1, 8).