GIVEN:
We are told that a baseball fan is sitting at a point where his eyes are 350 feet vertical distance from the ground. When the fan is looking at the home plate the angle of depression is 30 degrees.
Required;
Find the horizontal distance from the fan to the home plate.
Step-by-step solution;
We begin by making a sketch of the scene to determine the shape and angles formed. This is shown below;
From the sketch above we can see the that the baseball fan has effectively formed a right triangle with the home plate from his position and the dimensions, that is, angles and sides, have been labeled.
We have the reference angle given as 60 degrees and the opposite is x (horizontal distance from the fan to home plate). That means the adjacent side is 350.
We can now use the following trig ratio;
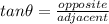
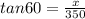
We now cross multiply;

A second way to determine this distance is by using the triangle formed by the angle 30 degrees, in which case the horizontal distance will be the green line as shown in the sketch above. In that case, the vertical distance of 350 feet will be the opposite while the horizontal distance will be the adjacent while the reference angle will be 30 degrees.
For the second scenario, the straight line distance between both sets of eyes is 300 feet, and the angle of depression is 48 degrees. Note that the second fan is being watched at an angle of depression of 48 degrees which means he is at a lower level.
Now we are required to determine the vertical distance between the field level and the eyes of the second fan.
Let us begin by calculating the value of x as indicated in the triangle.
We shall use the trig ratio of;
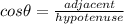
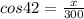
Now we cross multiply;

Observe carefully that the distance calculated as x (222.9 ft) is the vertical distance between both fans. If we subtract this value from 350 feet we will now derive the vertical distance from the second fan to the field level.
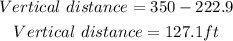
Therefore,
ANSWER:
