How much grain can a farmer hold in this silo? Use π = 3.14.A. 2,093.3 ft³B. 11,513.3 ft³C. 9,420 ft³D. 12,560.2 ft³

Question

asked Jun 20, 2023 162k views

1 Answer

OddEssay · Answer 1 · 2023-06-25T04:19:21+0000

To find out how much grain the farmer can hold we need to find the volume of the silo. The silo is made from a circular cylinder and half a sphere.

The volume of the cylinder is given by:

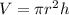
$V=\pi r^2h$

In this case r=10 and h=30, plugging this values in the equation above we have that the volume of the cylinder is:

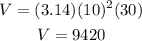
$\begin{gathered} V=(3.14)(10)^2(30) \\ V=9420 \end{gathered}$

Hence the volume of the cylinder is 9420 cubic feet.

Now we need to find the volume ot half the sphere, the volume og an sphere is given by:

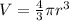
$V=(4)/(3)\pi r^3$

Plugging the radius we have that:

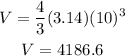
$\begin{gathered} V=(4)/(3)(3.14)(10)^3 \\ V=4186.6 \end{gathered}$

Now, we only need half this volume then the volume of the top of the silo is:

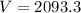
Finally we add the volume of the cylinder and half the sphere, therefore the volume of the sylo is:

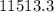
and the answer is B.