Step-by-step explanation
Coach Bennet must select 3 players out of a total of 14 players. The first thing to find is the number of different groups that he can select. The order of selection doesn't matter since being selected first, second or third doesn't change anything. This means that we must find the number of combinations when selecting 3 people out of a total of 14.
The number of combinations when selecting k items out of a total of n is given by the following formula:
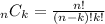
So if we want to find how many different selections the couch can make we must take k=3 and n=14:
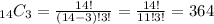
We then have to find the probability that couch bennet will select three juniors. This probability is given by the product of three probabilities:
- The probability that the first selected is a junior.
- The probability that the second selected is a junior.
- The probability that the third selected is a junior.
Each probability is given by the quotient between the number of non-selected juniors and the total number of non-selected players.
When the coach selects the first player there are 6 juniors out of 14 players. Then the first probability is 6/14. Assuming that he selected a junior when he has to select the second player there are 5 juniors out of 13 players (we are not counting the one that was already selected) so the second probability is 5/13. Then by the time he has to select a third player there are 4 non-selected juniors out of 12 non-selected players so the third probability is 4/12. Then the probability that couch bennet will select three juniors is given by the product of these three probabilities:
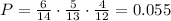
In order to express it as a percentage we must multiply it by 100:
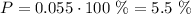
For the probability of selecting three seniors we can make an analogous calculation the only difference is that there are 8 initial non-selected seniors instead of 6 so we obtain:
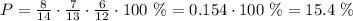
So the probability of selecting three seniors is greater.
If we want to find the total number of groups of three players where the three are juniors we must take into consideration that there is a total of 6 juniors. Then we must find the number of combinations when selecting 3 players out of 6:
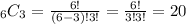
So this number can be expressed as ₆C₃ or as 20.
We then need to find the probaility that Jamie will be selected as the third player knowing that Taylor was already selected and that the other selected player is a senior.
By this time the coach has already selected two players so there are a total of 12 players including juniors and senior. Since the third player will be randomly selected independently of the group he belongs to the probability of selecting any given player is 1/12. Then the probability of selecting Jamie is:
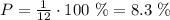
Answers
The answers for the first three drop-down menus are in bold:
"This is a combination because the order in which the players are selected isn't important. There are 364 different groups of three players possible for Coach Bennet to select."
The answers to the part with 6 different options are 20 and ₆C₃.
The answers for the other two drop-down menus are in bold:
"The probability that Coach Bennet will select three juniors is 5.5%. This probability is less than the probability that the coach will select three seniors."
The answer to part D is:
"The probability that Jamie will be selected as the third player, given that Taylor is selected as one of the first two players, is 8.3%.