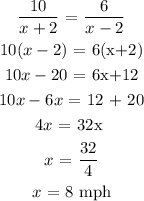The speed of the boat in still water is 8 mph
Here, we want to get the speed of the boat in still water
Here, we are going to bs using two speeds
The speed in moving water and the speed in still water
Let the speed of the boat in still water be x mph
The speed of the boat downstream is (x + 2) mph
The speed of the boat upstream is (x-2) mph
Mathematically,

From the question, we are told that the time taken to travel both upstream and downstream is the same
The time downstream is;

The time upstream is;
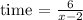
Since the times are equal, we equate the two as follows;