Solution:
From the question,
When price = $5.2, demand = 4500
When price = $5.9, demand = 2750
Assuming a linear demand curve,
We will have to determine the demand function (which is a linear function)
Using the knowledge of equation of a straight line given two points, we can determine the demand function to be
I.e when x = 5.2, y=4500
When x = 5.9, y = 2750
Thus, the equation is y = -2500x + 17500
In Demand function, we have
d = -2500p + 17500
Thus, the demand function is
d = -2500p + 17500
Revenue function = demand function x price
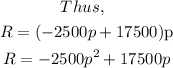
To determine the price that maximize the nightly hamburger revenue, plot the graph of Revenue function above and determine the value of p at the maximum point
The graph of Revenue function is shown below
From the graph, at maximum point, p = 3.5
Thus, the price that maximize the nightly hamburger revenue is $3.5