Question

Solve the system by graphing and determine the number of solutions it has. (Hint: to graph find the y-intercept and slope of the line.)

Answer 1

To graph a line, find two points that belong to that line, plot them into the coordinate plane and draw a line through them.

For instance, we can use x=0 to determine the corresponding value of y and then use y=0 to find the corresponding value of x, to plot the points.

For the first equation:

`\begin{gathered} y=2x-1 \\ x=0\Rightarrow y=-1 \\ y=0\Rightarrow2x=1\Rightarrow x=(1)/(2) \end{gathered}`

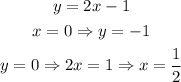
Then, the following points belong to the first line:

`\begin{gathered} (0,-1) \\ ((1)/(2),0) \end{gathered}`

Plot both boints on the coordinate plane and draw a line through them:

Use the same method to find two points over the second line.

`\begin{gathered} -6x+3y=-3 \\ x=0\Rightarrow3y=-3\Rightarrow y=-1 \\ y=0\Rightarrow-6x=-3\Rightarrow x=(1)/(2) \end{gathered}`

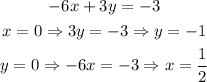
Then, the following points belong to the line:

`\begin{gathered} (0,-1) \\ ((1)/(2),0) \end{gathered}`

They turn out to be the same two points. Then, both lines overlap. Therefore, the system has infinite solutions.