The slope of a line, also known as the gradient of a line is the ratio of the change in the vertical values to the horizontal values of the given points.
The points given are
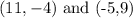
The horizontal values are
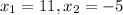
The vertical values are
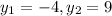
We can now apply the formula to compute the slope
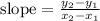
Hence
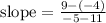
Thus
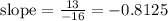
Thus, the slope rounded to the nearest tenths place will be
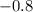
The slope is -0.8