Question

you are painting a panel with a dimond shaped window, as shown. you have to put up tape around the edge of the window to keep the paint off. find the length of tape you need to the nearest inch

Answer 1

In order to find the amount of tape needed, we need to find the perimeter of this quadrilateral. We can use the formula for the distance between two points to find the side lengths:

`d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}`

Using the points (24, 37) and (28, 40), we have:

`\begin{gathered} d=\sqrt[]{(40-37)^2+(28-24)^2} \\ d=\sqrt[]{3^2+4^2} \\ d=\sqrt[]{9+16} \\ d=\sqrt[]{25} \\ d=5 \end{gathered}`

Using the points (28, 40) and (32, 37):

`\begin{gathered} d=\sqrt[]{(37-40)^2+(32-28)^2} \\ d=\sqrt[]{(-3)^2+4^2} \\ d=\sqrt[]{25}=5 \end{gathered}`

Using the points (32, 37) and (28, 34):

`\begin{gathered} d=\sqrt[]{(34-37)^2+(28-32)^2} \\ d=\sqrt[]{(-3)^2+(-4)^2} \\ d=\sqrt[]{25}=5 \end{gathered}`

Using the points (28, 34) and (24, 37):

`\begin{gathered} d=\sqrt[]{(37-34)^2+(24-28)^2} \\ d=\sqrt[]{3^2+(-4)^2} \\ d=\sqrt[]{25}=5 \end{gathered}`

So all four sides of the figure have a length of 5 units, therefore the perimeter is:

`P=5+5=5+5=20\text{ in}`

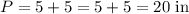
So the amount of tape needed is 20 inches.