We need to find the inverse of the following function:
y = 5x² - 4
This can be easily done by changing places of x and y variables like this:
x = 5y² - 4
Now we have to solve for y. I'm going to rewrite the equation:
5y² - 4 = x
Okay, we're good to go. Add 4 on both sides:
5y² = x + 4
Divide by 5 both sides:
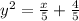
Sum the fractions on the right side:
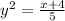
Take the square root on both sides:
![y=\pm\sqrt[]{(x+4)/(5)}](https://img.qammunity.org/2023/formulas/mathematics/college/vhvtzverlig9peq63bo91zqpqpe7p6val6.png)
And that's our inverse function.