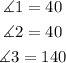Question

Find the measures of the numbered angles. (Hint: You may need to solve for x first!)10x + 10I3212x-16

Answer 1

To solve this problem we use the following property of angles in parallel lines:

If two lines are parallel (in this case the horizontal lines) the angles marked in the same color are equal.

Step 1. Identify the angles that are equal.

Using the previous property, we can find the angles that are equal:

Again, the angles in the same color are equal.

Step 2. Find an equation to solve for x.

Since the angle 10x+10 is equal to the angle 12x-16, the equation we have to solve is:

`12x-16=10x+10`

Step 3. Solve for x:

the first step to solve for x is to have the terms that contain the x on the same side of the equation, for that reason, we need to subtract 10x to both sides:

`12x-10x-16=10`

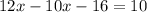
Combining the like terms on the left side:

`2x-16=10`

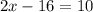
The next step to solve for x is to add 16 to both sides so that we have the x term alone on the left side:

`2x=10+16`

`2x=26`

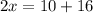
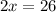
The last step to solve for x is to divide both sides by 2:

`\begin{gathered} x=(26)/(2) \\ x=13 \end{gathered}`

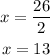
Step 4. To find angle 1 and 2 we need to find angle 10x+10 first:

`\begin{gathered} 10x+10 \\ \text{substituting x=13} \\ 10(13)+10 \\ 130+10 \\ 140 \end{gathered}`

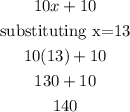
For reference, let's show this in the diagram:

Step 5. Since angle 1 is next to the 140° angle, we use the property that tells us that the sum of the angles on top of a line is 180°:

`140+\measuredangle1=180`

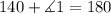
Solving for angle 1:

`\begin{gathered} \measuredangle1=180-140 \\ \measuredangle1=40 \end{gathered}`

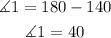
Step 6. Note that in the diagram ∡1 and ∡2 are in the same color, thus ∡1 and ∡2 are equal:

`\begin{gathered} \measuredangle1=\measuredangle2 \\ \sin ce\measuredangle1=40 \\ \measuredangle2=40 \end{gathered}`

Step 7. Find ∡3

As you can see on the diagram:

The red angles are equal.

This means that the 140° angle is equal to angle 3:

`\measuredangle3=140`

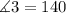
Answer:

`\begin{gathered} \measuredangle1=40 \\ \measuredangle2=40 \\ \measuredangle3=140 \end{gathered}`