Question

You invested $21,000 in two accounts paying 3% and 9% annual interest, respectively. If the total interest earned for the year was $810, how much was invested at each rate?

Answer 1

It was invested $18,000 at a 3% annual interest and $3,000 at a 9% annual interest.

Explanation:

To determine how much was invested at each rate, we can create a system of equations.

Let x be the amount invested at 3%

Let y be the amount invested at 9%

If the total invested was $21,000 and the interest earned was $810

`\begin{gathered} \text{0}.03x+0.09y=810 \\ \text{ Then, if} \\ y=21,000-x \end{gathered}`

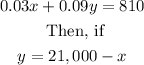
Substitute y into the first equation, and solve for x.

`\begin{gathered} 0.03x+0.09(21000-x)=810 \\ 0.03x+1890-0.09x=810 \\ \text{0}.09x-0.03x=1890-810 \\ 0.06x=1080 \\ x=(1,080)/(0.06) \\ x=\text{ \$18,000} \end{gathered}`

Now, if x=18,000, substitute it into the y-equation:

`\begin{gathered} y=21000-18000 \\ y=\text{ \$3,000} \end{gathered}`

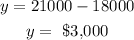
It was invested $18,000 at a 3% annual interest and $3,000 at a 9% annual interest.