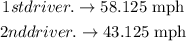
Step-by-step explanation
Step 1
time= 4 hours
total distance = x+y=415

so,for car 1
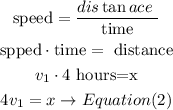
Now, for car 2
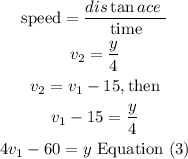
Step 2
solve the equations
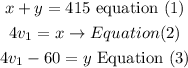
a) replace x value from equation (3) and (2) in equation (1)

so, the speed of the first car is 58.125 mpj, now replace the v1 , to find v2
The first driver is traveling 15 mph faster than the second driver
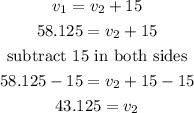
Hence
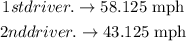
I hope this helps you