Given
The equations are,
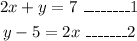
To find the slope intercept form and to check whether the lines are parallel or perpendicular.
Step-by-step explanation:
It is given that,
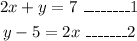
Since the slope intercept form is defined as,
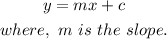
Then, (1) can be written as,
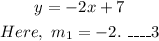
And, (2) can be written as,
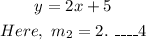
From (3) and (4),
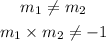
Hence, the equations are neither parallel nor perpendicular.