Question

NO LINKS!! Please help me with this problem 2b​

Answer 1

`\textsf{a)} \quad 27.9 \pm 0.15`

Step-by-step explanation:

Given values:

• Sample size n = 450
• Population standard deviation σ = 1.6
• Sample mean
  `\overline{x}` = 27.9

`\boxed{\begin{minipage}{7 cm}\underline{Standard error of the mean}\\\\$SE=(\sigma)/(√(n))$\\\\where:\\\phantom{ww}$\bullet$ $\sigma$ is the population standard deviation. \\ \phantom{ww}$\bullet$ $n$ is the sample size.\\\end{minipage}}`

Substitute the given values into the standard error formula:

`\implies SE=(1.6)/(√(450))=(4√(2))/(75)`

The critical value for a 95% confidence level using normal distribution is:

`z=1.9600\;\;\sf (4\;d.p.)`

`\boxed{\begin{minipage}{6.7 cm}\underline{Margin of error}\\\\$ME=z \cdot SE$\\\\where:\\\phantom{ww}$\bullet$ $z$ is the critical value. \\ \phantom{ww}$\bullet$ $SE$ is the standard error of the mean.\\\end{minipage}}`

Substitute the given values into the margin of error formula:

`\implies ME=1.9600 \cdot (4√(2))/(75)`

`\implies ME=0.15\;\; \sf (2\;d.p.)`

Therefore, an estimate for the size of the population mean, including margin or error is:

`\implies \mu=\overline{x}\pm ME`

`\implies \mu=27.9 \pm 0.15`

Answer 2

Answer: Choice A)
`\boldsymbol{27.9 \ \pm \ 0.15}`

======================================================

Step-by-step explanation:

xbar = 27.9 = sample mean

n = 450 = sample size

sigma = 1.6 = population standard deviation

Your teacher didn't mention the confidence level, so let's assume it's the default of 95%. At this level, the critical z value is roughly z = 1.96

Let's find the margin of error.

E = z*sigma/sqrt(n)

E = 1.96*1.6/sqrt(450)

E = 0.14783245772007

E = 0.15

If your teacher wanted you to use z = 2 instead of z = 1.96, then,

E = z*sigma/sqrt(n)

E = 2*1.6/sqrt(450)

E = 0.15084944665313

E = 0.15

We get the same approximate value of E when rounding to two decimal places.

Therefore, the confidence interval estimating mu in the format
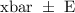`\text{xbar} \ \pm \ \text{E}` is approximately
`\boldsymbol{27.9 \ \pm \ 0.15}` which points us to choice A as the final answer.