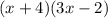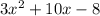
To factor an equation in the form:
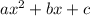
1. You can start by factor the term b as the add of two terms that multiplying give: -24
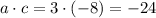
and the adding = 10
in this case could be 12 and -2
you get:
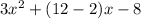
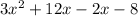
2. You can factor then finding the greatest common denominator by grouping the first two terms and the last two:
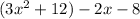
To the first two terms you have the gratest common denominator 3x and the second gruop -2
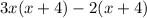
Then you finally factor the greatest common denominator:
The final factor is: