Answer: Choice B)

======================================================
Step-by-step explanation:
sigma = 1.2 = population standard deviation
n = 200 = sample size
Your teacher doesn't mention the confidence level, so I'll assume we go for the default 95%.
At 95% confidence, the z critical value is roughly z = 1.96
The margin of error (E) is calculated like so:
E = z*sigma/sqrt(n)
E = 1.96*1.2/sqrt(200)
E = 0.1663 approximately
That rounds to 0.17
Therefore the estimate for the population mean in the format
 is
is
 which is the final answer.
which is the final answer.
------------
This is the shorthand way of saying the mean mu is between
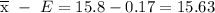 and
and
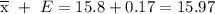
In other words,
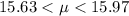 at 95% confidence.
at 95% confidence.