Use the discriminant to find the nature of the solutions to the following quadratic equation
3x^2 +x-3=0
Two imaginary number solutions
one repeated rational solution
one repeated irrational number solution
Two different irrational number solutions
Two different rational number solutions.
we know that
the discriminant of a quadratic equation is
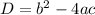
we have
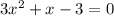
so
a=3
b=1
c=-3
substitute in the equation Of discriminant
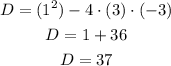
we have that
D >0
that means
Two different rational number solutions