From the reaction, each Pb(SO₄)₂ reacts with 4 LiNO₃.
So, first, we need to figure ot how many moles of Pb(SO₄)₂ we have in 2.35 grams.
For this, we need to use the molar masses of its elements to find its molar mass:
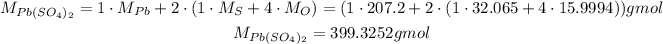
Using it, we can calcualte the number of moles of Pb(SO₄)₂:
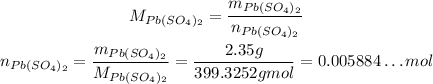
Using the stoichiometry, we have:
LiNO₃ --- Pb(SO₄)₂
4 --- 1
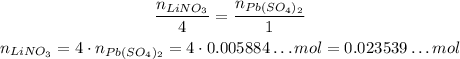
Now that we know the number of moles of LiNO₃, we can calculate how many LiNO₃ are needed by using the Avogadro's Number:
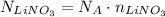
Avogadro's Number is approximately 6.022 x 10²³ mol⁻¹, so, using this value, we have:
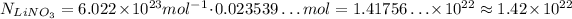
So, we need approximately 1.42 x 10²² LiNO₃.