Question

A wind-up toy car has a mass of 66 g. The car is wound, and then released, going from being at rest to a constant velocity of 0.7 m/s. If the internal force of thewinding on the tires is 0.44 N, what is the duration of the impulse imparted by the winding on the car.

Answer 1

0.105 seconds

Step-by-step explanation:

The impulse is equal to the change in the momentum and it is also equal to the force times time, so

`\begin{gathered} I=Ft=p_f-p_i \\ Ft=m_{}v_f-mv_i_{} \end{gathered}`

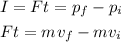
Where F is the force, t is the time, m is the mass, vf is the final velocity and vi is the initial velocity. Solving for t, we get

`t=(mv_f-mv_i)/(F)`

So, replacing m = 66g = 0.066 kg, vf = 0.7 m/s and vi = 0 m/s because it begins at rest and F = 0.44 N, we get

Therefore, the duration of the impulse imparted was 0.105 seconds