Given a quadratic equation:

the expression to find the axis of symmetry is:

in this case, for the first equation, we have the following:

for the second equation, we get:
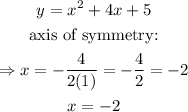
as we can see, both functions have the same axis of symmetry, that's why you cannot distinguish them. In general, several quadratic functions can have the same axis of symmetry, without being equivalent between each other.