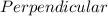Question

Just these need to be done appreciate it Number 12

Answer 1

Step-by-step explanation:

The coordinates are given below as

`\begin{gathered} Q(-6,11) \\ R(2,-1) \\ S(-4,8) \\ T(-1,10) \end{gathered}`

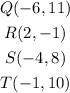
Concept:

Rule for perpendicularity,

`m_1* m_2=-1`

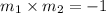
Rule for parallelism

`m_1=m_2`

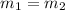
Step 1:

We will calculate the slope of QR using the formula below

`m_1=(y_2-y_1)/(x_2-x_1)`

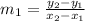
By substituting the values, we will have

`\begin{gathered} m_(1)=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ m_1=(-1-11)/(2-(-6)) \\ m_1=-(12)/(2+6) \\ m_1=-(12)/(8) \\ m_1=-(3)/(2) \end{gathered}`

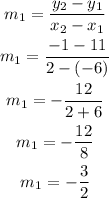
Step 2:

Calculate the slope of RT using the formula below

`\begin{gathered} m_2=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \end{gathered}`

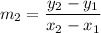
By substituting the values, we will have

`\begin{gathered} m_2=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ m_2=(10-8)/(-1-(-4)) \\ m_2=(2)/(-1+4) \\ m_2=(2)/(3) \end{gathered}`

Hence,

`\begin{gathered} m_1\\e m_2(not\text{ }parllel) \\ m_1* m_2=-(3)/(2)*(2)/(3)=-1 \end{gathered}`

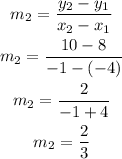
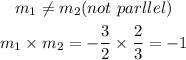
Hence,

The final answer is

`Perpendicular`