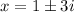Question

Find the solutions to x2-2x+10=0. The quadratic formula has been started for you.

Answer 1

The solution to the quadratic equation is

`x=1\pm3i`

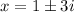
Step-by-step explanation

Problem Statement

The question gives us the beginning of the application of the Quadratic formula on a quadratic equation. We are required to simplify the expression and get in more certain terms, the values of x.

The expression given is:

`\begin{gathered} x^2-2x+10=0 \\ \\ x=\frac{2\pm\sqrt[]{(-2)^2-(4)(1)(10)}}{2} \end{gathered}`

Solution

Let us begin to simplify the expression below:

`\begin{gathered} x=\frac{2\pm\sqrt[]{(-2)^2-(4)(1)(10)}}{2} \\ \\ x=\frac{2\pm\sqrt[]{(-2*-2)^{}-(4*1*10)}}{2} \\ \\ x=\frac{2\pm\sqrt[]{4-40}_{}}{2} \\ \\ x=\frac{2\pm\sqrt[]{-36}}{2} \\ \\ \text{From the laws of indices, we have:} \\ \sqrt[]{a* b}=\sqrt[]{a}*\sqrt[]{b} \\ \\ x=\frac{2\pm\sqrt[]{-1*36}}{2} \\ \\ x=\frac{2\pm(\sqrt[]{-1})(\sqrt[]{36})}{2} \\ \\ \text{ We know that, } \\ \sqrt[]{-1}=i \\ \\ x=(2\pm(i)(6))/(2) \\ \\ x=(2\pm6i)/(2) \\ \\ x=(2(1\pm3i))/(2) \\ \\ 2\text{ Crosses out} \\ \\ x=1\pm3i \end{gathered}`

Final Answer

The solution to the quadratic equation is

`x=1\pm3i`