Step-by-step explanation
To solve this problem, we must apply Bayes Theorem, which states that:
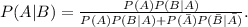
We define the events:
• A = has the disease,
,
• B = test positive.
From the statement, we know that:
• the disease has an incidence rate of 0.1% → P(A) = 0.1% = 0.001 → P(not A) = 99.9% = 0.999,
• anyone who has the disease will test positive → P(B | A) = 100% = 1,
• the false positive rate is 1% → P(not A) = 1% = 0.01,
,
• the false-negative rate is 6% → P(not B | not A) = 6% = 0.06.
Replacing these values in the formula above, we get:
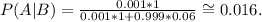
Answer
The probability that a person who tests positive actually has the disease is approximately 0.016.