Question

Simplify each expression. (by using the reciprocal identities, quotient identities, and pythagorean identities.)

Answer 1

37)

`(\sec x)/(\tan x+\cot x)`

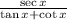
First, we will simplify the denominator

tanx + cot x

tanx = sinx/cosx and cotx = cosx / sinx

`(\sin x)/(\cos x)+(\cos x)/(\sin x)=\frac{\sin ^2x+\cos ^2x}{\text{cosxsinx}}`

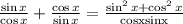
sin²x +cos²x = 1

`=(1)/(\cos x\sin x)`

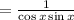
substitute back to the original expression

`(\sec x)/(\cos x\sin x)`

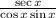
but secx = 1/cosx

`(1)/(\cos x)dividedby(1)/(\cos x\sin x)`
`=(1)/(\cos x)*\cos x\sin x`

`=\sin x`

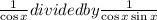
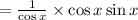
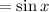
39)

`(1-\sin ^2x)/(\cos x)`

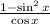
1 - sin²x = cos²x

substitute the above into the original expression

`(\cos ^2x)/(\cos x)`

`=\cos \text{ x}`

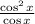
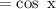
40)

`(\csc ^2x-1)/(\csc ^2x)`

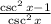
csc²x - 1 = cot²x

substitute the above into the original expression

`(\cot^2x)/(\csc^2x)`

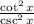
But 1 + tan²x = cot²x

1 + tan²x

= 1 + sin²x/cos²x

= sin²x+cos²x /cos²x

=1 /cos²x

substitute into the expression

`((1)/(\cos^2x))/(\csc ^2x)`

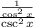
1/cos²x ÷ csc²x

but csc²x = 1/sin²x

1/cos²x ÷ 1/sin²x

1/cos²x (sin²x)

`(\sin ^2x)/(\cos ^2x)`

`=\tan ^2x`

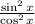
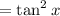
38)

`(1+\sin x)/(\cos x)+(\cos x)/(\sin x-1)`

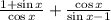
Find the lcm

`((\sin x-1)(1+\sin x)+(\cos x)(\cos x))/(\cos x(\sin x-1))`

`(\sin x+\sin ^2x-1-\sin x+\cos ^2x)/(\cos x(\sin x-1))`

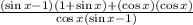
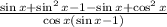
Re-arrange the numerator

`(\sin x-\sin x-1+\sin ^2x+\cos ^2x)/(\cos x(\sin x-1))`
`(-1+\sin ^2x+\cos ^2x)/(\cos x(\sin x-1))`

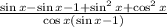
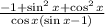
But, sin²x+cos²x=1

`(-1+1)/(\cos x(\sin x-1))`

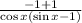
= 0