Question

(a) How high is the ball when it was thrown?(b) What is the maximum height of the ball?

Answer 1

Given:

`h(x)=-(1)/(20)x^2+8x+6`

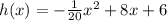
Where h(x) is the height of the ball that is thrown in the air

And (x) is the horizontal distance in feet from the point of throwing

We will find the following:

(a) How high is the ball when it was thrown?

So, substitute with x = 0

So, h(x) = 6

So, the answer to part (a) is 6 feet

(b) What is the maximum height of the ball?

So, as the function h(x) is a quadratic function, we will find the vertex point

We will complete the square of h(x):

`\begin{gathered} h(x)=-(1)/(20)(x^2-160x)+6 \\ h(x)=-(1)/(20)(x^2-160x+6400-6400)+6 \\ \\ h(x)=-(1)/(20)(x^2-160x+80^2)+(6400)/(20)+6 \\ \\ h(x)=-(1)/(20)(x-80)^2+326 \end{gathered}`

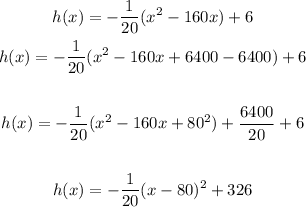
So, the vertex of h(x) will be = (80, 326)

So, the answer of part b) the maximum height = 326 feet